Polarisaatio on yksi antennien perusominaisuuksista. Meidän on ensin ymmärrettävä tasoaaltojen polarisaatio. Sen jälkeen voimme keskustella antennien polarisaation päätyypeistä.
lineaarinen polarisaatio
Alamme ymmärtää tasomaisen sähkömagneettisen aallon polarisaatiota.
Tasomaisella sähkömagneettisella (EM) aallolla on useita ominaisuuksia. Ensimmäinen on, että teho kulkee yhteen suuntaan (kenttä ei muutu kahdessa ortogonaalisessa suunnassa). Toiseksi sähkökenttä ja magneettikenttä ovat kohtisuorassa toisiinsa nähden ja ortogonaalisia toisiinsa nähden. Sähkö- ja magneettikentät ovat kohtisuorassa tasoaallon etenemissuuntaan nähden. Esimerkkinä tarkastellaan yhtälön (1) mukaista yksitaajuista sähkökenttää (E-kenttä). Sähkömagneettinen kenttä kulkee +z-suunnassa. Sähkökenttä suuntautuu +x-suuntaan. Magneettikenttä on +y-suuntainen.
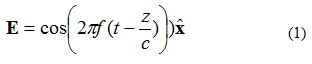
Huomioi yhtälössä (1) merkintätapa: . Tämä on yksikkövektori (pituusvektori), joka osoittaa, että sähkökentän piste on x-suunnassa. Tasoaalto on esitetty kuvassa 1.
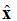
kuva 1. Sähkökentän graafinen esitys +z-suunnassa.
Polarisaatio on sähkökentän jälki ja etenemismuoto (ääriviiva). Tarkastellaan esimerkkinä tasoaallon sähkökentän yhtälöä (1). Tarkastelemme sähkökentän sijaintia (X,Y,Z) = (0,0,0) ajan funktiona. Tämän kentän amplitudi on esitetty kuvassa 2 useina ajankohtina. Kenttä värähtelee taajuudella "F".
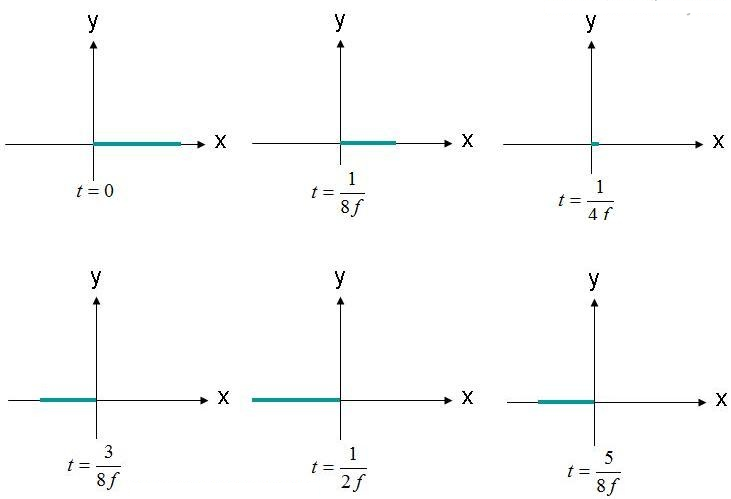
kuva 2. Tarkkaile sähkökenttää (X, Y, Z) = (0,0,0) eri ajankohtina.
Sähkökenttä havaitaan origossa, ja se värähtelee amplitudiltaan edestakaisin. Sähkökenttä on aina osoitetun x-akselin suuntainen. Koska sähkökenttä ylläpidetään yhden linjan suuntaisesti, kentän voidaan sanoa olevan lineaarisesti polarisoitunut. Lisäksi, jos X-akseli on yhdensuuntainen maanpinnan kanssa, tätä kenttää kuvataan myös vaakasuoraan polarisoituneeksi. Jos kenttä on suunnattu Y-akselin suuntaisesti, aallon voidaan sanoa olevan pystysuoraan polarisoitunut.
Lineaarisesti polarisoitujen aaltojen ei tarvitse olla suunnattu vaaka- tai pystysuoraa akselia pitkin. Esimerkiksi sähkökentän aalto, jonka rajoitus on kuvan 3 mukaisesti suoran suuntainen, olisi myös lineaarisesti polarisoitu.
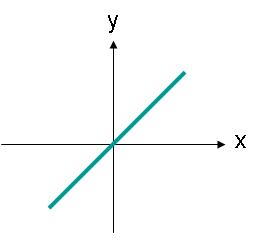
kuva 3. Lineaarisesti polarisoidun aallon sähkökentän amplitudi, jonka lentorata on kulma.
Kuvassa 3 esitettyä sähkökenttää voidaan kuvata yhtälöllä (2). Sähkökentässä on nyt x- ja y-komponentti. Molemmat komponentit ovat kooltaan yhtä suuret.
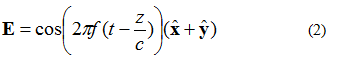
Yksi yhtälön (2) huomioitava seikka on toisen vaiheen xy-komponentti ja elektronikentät. Tämä tarkoittaa, että molemmilla komponenteilla on sama amplitudi koko ajan.
pyöreä polarisaatio
Oletetaan nyt, että tasoaallon sähkökenttä on yhtälön (3) mukainen:
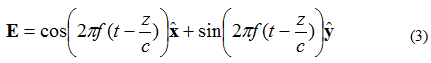
Tässä tapauksessa X- ja Y-elementit ovat 90 asteen vaihesiirrossa. Jos kenttä havaitaan muodossa (X, Y, Z) = (0,0,0) jälleen kuten aiemmin, sähkökentän ja ajan käyrä näyttää alla olevan kuvan 4 mukaiselta.
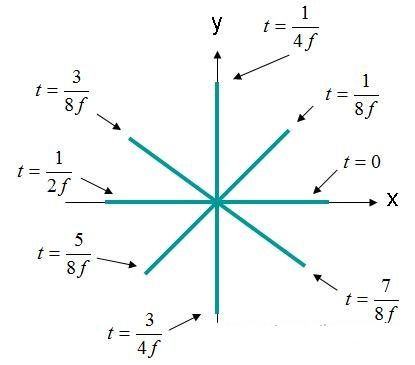
Kuva 4. Sähkökentän voimakkuus (X, Y, Z) = (0,0,0) EQ-alue. (3).
Kuvassa 4 esitetty sähkökenttä pyörii ympyrää. Tämän tyyppistä kenttää kuvataan ympyräpolarisoituna aallona. Ympyräpolarisaation on täytettävä seuraavat kriteerit:
- Pyöreän polarisaation standardi
- Sähkökentässä on oltava kaksi ortogonaalista (kohtisuoraa) komponenttia.
- Sähkökentän ortogonaalisilla komponenteilla on oltava yhtä suuret amplitudit.
- Kvadratuurikomponenttien on oltava 90 asteen vaihesiirrossa.
Jos kenttä liikkuu aaltokuvion 4 näytöllä, kentän rotaation sanotaan olevan vastapäivään ja oikealle pyörivästi polarisoitunut (RHCP). Jos kenttä kiertyy myötäpäivään, kenttä on vasemmalle pyörivästi polarisoitunut (LHCP).
Elliptinen polarisaatio
Jos sähkökentässä on kaksi toisiinsa nähden kohtisuoraa komponenttia, jotka ovat 90 asteen vaihe-erossa, mutta yhtä suuret, kenttä on elliptisesti polarisoitu. Tarkastellaan +z-suunnassa kulkevan tasoaallon sähkökenttää yhtälöllä (4):
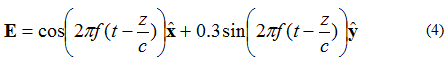
Sähkökentän vektorin kärjen sijaintipiste on esitetty kuvassa 5.
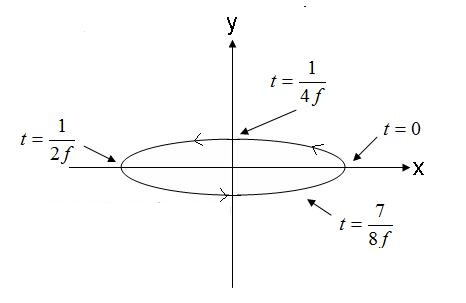
Kuva 5. Prompt-elliptisen polarisaatioaallon sähkökenttä. (4).
Kuvassa 5 esitetty kenttä, joka kulkee vastapäivään, olisi oikealle kääntyvä elliptinen, jos se kulkisi ulos kuvaruudusta. Jos sähkökentän vektori pyörii vastakkaiseen suuntaan, kenttä on vasemmalle kääntyvästi elliptisesti polarisoitunut.
Lisäksi elliptinen polarisaatio viittaa sen epäkeskisyyteen. Epäkeskisyyden suhde pää- ja sivuakselien amplitudiin. Esimerkiksi yhtälön (4) mukainen aallon epäkeskisyys on 1/0,3 = 3,33. Elliptisesti polarisoituja aaltoja kuvataan edelleen pääakselin suunnalla. Aaltoyhtälöllä (4) on akseli, joka koostuu pääasiassa x-akselista. Huomaa, että pääakseli voi olla missä tahansa tasokulmassa. Kulman ei tarvitse sopia X-, Y- tai Z-akseliin. Lopuksi on tärkeää huomata, että sekä ympyrä- että lineaarinen polarisaatio ovat elliptisen polarisaation erikoistapauksia. 1.0 epäkeskinen elliptisesti polarisoitu aalto on ympyräpolarisoitu aalto. Elliptisesti polarisoidut aallot, joilla on ääretön epäkeskisyys. Lineaarisesti polarisoidut aallot.
Antennin polarisaatio
Nyt kun olemme tietoisia polarisoiduista tasoaallon sähkömagneettisista kentistä, antennin polarisaatio on yksinkertaisesti määritelty.
Antennin polarisaatio Antennin kaukokentän arviointi, syntyvän säteilevän kentän polarisaatio. Siksi antennit luokitellaan usein "lineaarisesti polarisoiduiksi" tai "oikeakätisiksi ympyräpolarisoiduiksi antenneiksi".
Tämä yksinkertainen käsite on tärkeä antenniviestinnässä. Ensinnäkin vaakasuoraan polarisoitu antenni ei kommunikoi pystysuoraan polarisoidun antennin kanssa. Vastavuoroisuuslauseen vuoksi antenni lähettää ja vastaanottaa täsmälleen samalla tavalla. Siksi pystysuoraan polarisoidut antennit lähettävät ja vastaanottavat pystysuoraan polarisoituja kenttiä. Siksi, jos yrität välittää pystysuoraan polarisoitua vaakasuoraan polarisoitua antennia, vastaanottoa ei ole.
Yleisessä tapauksessa kahdelle lineaarisesti polarisoidulle antennille, jotka ovat kiertyneet toisiinsa nähden kulman ( ) verran, tästä polarisaatio-epäsuhdasta johtuva tehohäviö kuvataan polarisaatiohäviökertoimella (PLF):
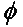
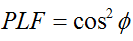
Näin ollen, jos kahdella antennilla on sama polarisaatio, niiden säteilevien elektronikenttien välinen kulma on nolla, eikä polarisaatio-epäsuhdan vuoksi synny tehohäviötä. Jos toinen antenni on pystysuunnassa ja toinen vaakasuunnassa polarisoitu, kulma on 90 astetta, eikä tehoa siirry.
HUOMAUTUS: Puhelimen siirtäminen pään yläpuolella eri kulmiin selittää, miksi kuuluvuus voi joskus parantua. Matkapuhelinten antennit ovat yleensä lineaarisesti polarisoituja, joten puhelimen kääntäminen voi usein vastata puhelimen polarisaatiota ja parantaa siten kuuluvuutta.
Ympyräpolarisaatio on monien antennien toivottu ominaisuus. Molemmat antennit ovat ympyräpolarisoituja, eivätkä ne kärsi signaalin häviöstä polarisaatio-epäsuhdan vuoksi. GPS-järjestelmissä käytettävät antennit ovat oikealle ympyräpolarisoituja.
Oletetaan nyt, että lineaarisesti polarisoitu antenni vastaanottaa ympyräpolarisoituja aaltoja. Oletetaan vastaavasti, että ympyräpolarisoitu antenni pyrkii vastaanottamaan lineaarisesti polarisoituja aaltoja. Mikä on tuloksena oleva polarisaatiohäviökerroin?
Muista, että ympyräpolarisaatio on itse asiassa kaksi ortogonaalista lineaarisesti polarisoitua aaltoa, jotka ovat 90 astetta vaiheen ulkopuolella. Siksi lineaarisesti polarisoitu (LP) antenni vastaanottaa vain ympyräpolarisoidun (CP) aallon vaihekomponentin. Siksi LP-antennin polarisaation epäsuhtahäviö on 0,5 (-3 dB). Tämä pätee riippumatta siitä, mihin kulmaan LP-antennia käännetään. Siksi:
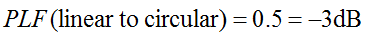
Polarisaatiohäviökerrointa kutsutaan joskus polarisaatiotehokkuudeksi, antennin epäsuhtakertoimeksi tai antennin vastaanottokertoimeksi. Kaikki nämä nimet viittaavat samaan käsitteeseen.
Julkaisun aika: 22.12.2023







