Kun on kyseantennit, kysymys, josta ihmiset ovat eniten huolissaan, on "Miten säteily oikeastaan saavutetaan?" Kuinka signaalilähteen synnyttämä sähkömagneettinen kenttä etenee siirtolinjan läpi ja antennin sisällä ja lopulta "erkanee" antennista muodostaen vapaan tilan aallon.
1. Yksijohtiminen säteily
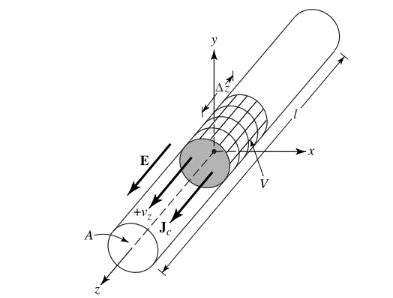
Oletetaan, että varaustiheys, ilmaistuna qv:nä (Coulomb/m3), on tasaisesti jakautunut pyöreään johtoon, jonka poikkileikkauspinta-ala on a ja tilavuus V, kuten kuvassa 1 on esitetty.
Kuva 1
Kokonaisvaraus Q tilavuudessa V liikkuu z-suunnassa tasaisella nopeudella Vz (m/s). Voidaan todistaa, että virrantiheys Jz johtimen poikkileikkauksella on:
Jz = qv vz (1)
Jos lanka on valmistettu ideaalisesta johtimesta, virrantiheys Js langan pinnalla on:
Js = qs vz (2)
Missä qs on pintavaraustiheys. Jos lanka on hyvin ohut (ihannetapauksessa säde on 0), langan virta voidaan ilmaista seuraavasti:
Iz = ql vz (3)
Jossa ql (coulomb/metri) on varaus pituusyksikköä kohti.
Käsittelemme pääasiassa ohuita lankoja, ja johtopäätökset pätevät edellä mainittuihin kolmeen tapaukseen. Jos virta on ajassa muuttuva, kaavan (3) derivaatta ajan suhteen on seuraava:
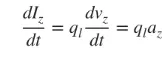
(4)
az on varauskiihtyvyys. Jos langan pituus on l, yhtälö (4) voidaan kirjoittaa seuraavasti:
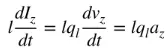
(5)
Yhtälö (5) kuvaa virran ja varauksen välistä perussuhdetta sekä sähkömagneettisen säteilyn perussuhdetta. Yksinkertaisesti sanottuna säteilyn tuottamiseksi tarvitaan ajassa muuttuvaa virtaa tai varauksen kiihtyvyyttä (tai hidastuvuutta). Yleensä mainitsemme virran aikaharmonisissa sovelluksissa, ja varaus mainitaan useimmiten transienttisovelluksissa. Varauksen kiihtyvyyden (tai hidastuvuuden) tuottamiseksi lanka on taivutettava, taitettava ja epäjatkuva. Kun varaus värähtelee aikaharmonisessa liikkeessä, se tuottaa myös jaksollista varauksen kiihtyvyyttä (tai hidastuvuutta) tai ajassa muuttuvaa virtaa. Siksi:
1) Jos varaus ei liiku, virtaa ei kulje eikä säteilyä synny.
2) Jos varaus liikkuu vakionopeudella:
a. Jos lanka on suora ja äärettömän pitkä, säteilyä ei tapahdu.
b. Jos lanka on taipunut, taittunut tai epäjatkuva, kuten kuvassa 2 on esitetty, säteilyä esiintyy.
3) Jos varaus värähtelee ajan kuluessa, se säteilee, vaikka lanka olisi suora.
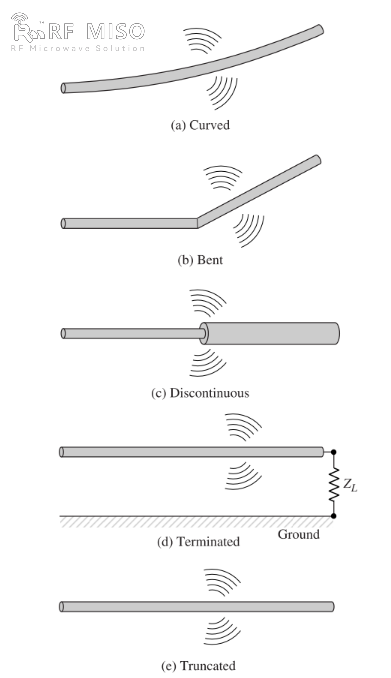
Kuva 2
Säteilymekanismin laadullinen ymmärtäminen voidaan saada tarkastelemalla pulssitettua lähdettä, joka on kytketty avoimeen johtimeen, joka voidaan maadoittaa kuorman kautta avoimesta päästään, kuten kuvassa 2(d) on esitetty. Kun johdin aluksi käynnistetään, lähteen synnyttämät sähkökenttäviivat laittavat johtimen varaukset (vapaat elektronit) liikkeelle. Kun varaukset kiihtyvät johtimen lähteen puoleisessa päässä ja hidastuvat (negatiivinen kiihtyvyys suhteessa alkuperäiseen liikkeeseen) heijastuessaan johtimen päästä, sen päihin ja muualle johtimeen syntyy säteilykenttä. Varausten kiihtyvyys saadaan aikaan ulkoisella voimanlähteellä, joka laittaa varaukset liikkeelle ja tuottaa niihin liittyvän säteilykentän. Varausten hidastuvuus johtimen päissä saadaan aikaan indusoituun kenttään liittyvien sisäisten voimien avulla, jotka johtuvat keskittyneiden varausten kertymisestä johtimen päihin. Sisäiset voimat saavat energiaa varauksen kertymisestä, kun sen nopeus laskee nollaan johtimen päissä. Siksi sähkökentän herätteen aiheuttama varausten kiihtyvyys ja johtimen impedanssin epäjatkuvuuden tai tasaisen käyrän aiheuttama varausten hidastuvuus ovat sähkömagneettisen säteilyn syntymismekanismeja. Vaikka sekä virrantiheys (Jc) että varaustiheys (qv) ovat lähdetermejä Maxwellin yhtälöissä, varausta pidetään perustavanlaatuisempana suureena, erityisesti transienttikentissä. Vaikka tätä säteilyn selitystä käytetään pääasiassa transienttitiloihin, sitä voidaan käyttää myös tasapainotilan säteilyn selittämiseen.
Suosittele useita erinomaisiaantennituotteetvalmistajaRFMISO:
2. Kaksijohtiminen säteily
Kytke jännitelähde antenniin kytkettyyn kaksijohtimiseen siirtolinjaan, kuten kuvassa 3(a) on esitetty. Jännitteen kohdistaminen kaksijohtimiseen linjaan synnyttää sähkökentän johtimien välille. Sähkökentän viivat vaikuttavat kuhunkin johtimeen kytkettyihin vapaisiin elektroneihin (jotka on helppo erottaa atomeista) ja pakottavat ne liikkumaan. Varausten liike synnyttää virtaa, joka puolestaan synnyttää magneettikentän.
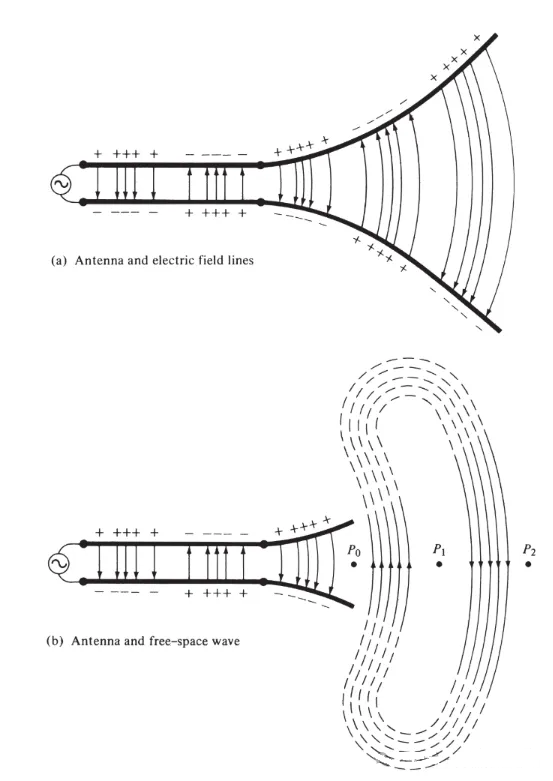
Kuva 3
Olemme hyväksyneet ajatuksen, että sähkökentän viivat alkavat positiivisilla varauksilla ja päättyvät negatiivisiin varauksiin. Tietenkin ne voivat myös alkaa positiivisilla varauksilla ja päättyä äärettömyyteen; tai alkaa äärettömyydestä ja päättyä negatiivisiin varauksiin; tai muodostaa suljettuja silmukoita, jotka eivät ala eivätkä pääty mihinkään varaukseen. Magneettikentän viivat muodostavat aina suljettuja silmukoita virtaa johtavien johtimien ympärille, koska fysiikassa ei ole magneettisia varauksia. Joissakin matemaattisissa kaavoissa ekvivalentteja magneettisia varauksia ja magneettivirtoja käytetään osoittamaan teho- ja magneettilähteisiin liittyvien ratkaisujen dualismia.
Kahden johtimen väliin piirretyt sähkökentän viivat auttavat havainnollistamaan varauksen jakautumista. Jos oletamme, että jännitelähde on sinimuotoinen, odotamme johtimien välisen sähkökentän olevan myös sinimuotoinen ja sen jakso on yhtä suuri kuin lähteen jakso. Sähkökentän voimakkuuden suhteellista suuruutta edustaa sähkökentän viivojen tiheys, ja nuolet osoittavat suhteellisen suunnan (positiivinen tai negatiivinen). Ajassa muuttuvien sähkö- ja magneettikenttien syntyminen johtimien välillä muodostaa sähkömagneettisen aallon, joka etenee siirtolinjaa pitkin, kuten kuvassa 3(a) on esitetty. Sähkömagneettinen aalto saapuu antenniin varauksen ja vastaavan virran mukana. Jos poistamme osan antennin rakenteesta, kuten kuvassa 3(b) on esitetty, vapaan tilan aalto voidaan muodostaa "yhdistämällä" sähkökentän viivojen avoimet päät (esitetty katkoviivoilla). Vapaan tilan aalto on myös jaksollinen, mutta vakiovaiheinen piste P0 liikkuu ulospäin valonnopeudella ja kulkee λ/2 matkan (pisteeseen P1) puolessa ajassa. Lähellä antennia vakiovaiheinen piste P0 liikkuu valonnopeutta nopeammin ja lähestyy valonnopeutta kaukana antennista olevissa pisteissä. Kuva 4 esittää λ∕2-antennin vapaan tilan sähkökentän jakauman ajanhetkellä t = 0, t/8, t/4 ja 3T/8.
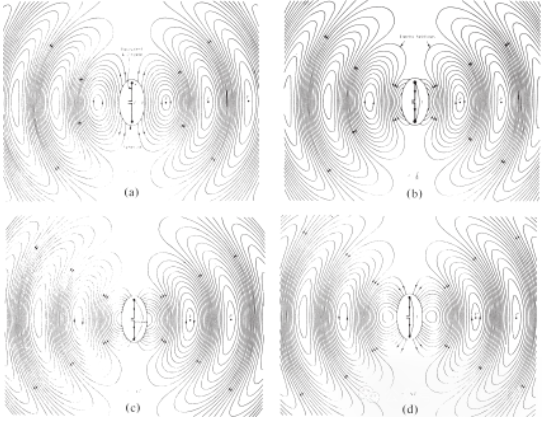
Kuva 4. λ∕2-antennin vapaan tilan sähkökentän jakauma ajanhetkellä t = 0, t/8, t/4 ja 3T/8.
Ei tiedetä, miten ohjautuneet aallot irtoavat antennista ja lopulta muodostuvat leviämään vapaassa tilassa. Voimme verrata ohjautuneita ja vapaassa tilassa olevia aaltoja veden aaltoihin, joita voi aiheuttaa tyyneen veteen pudonnut kivi tai muulla tavoin. Kun häiriö vedessä alkaa, veden aallot syntyvät ja alkavat levitä ulospäin. Vaikka häiriö loppuisi, aallot eivät pysähdy, vaan jatkavat etenemistä eteenpäin. Jos häiriö jatkuu, uusia aaltoja syntyy jatkuvasti, ja näiden aaltojen eteneminen on jäljessä muista aalloista.
Sama pätee sähköisten häiriöiden synnyttämiin sähkömagneettisiin aaltoihin. Jos lähteestä tuleva alkuperäinen sähköinen häiriö on lyhytkestoinen, syntyvät sähkömagneettiset aallot etenevät siirtolinjan sisällä, tulevat sitten antenniin ja lopulta säteilevät vapaan tilan aaltoina, vaikka herätettä ei enää olisikaan (aivan kuten vesiaallot ja niiden aiheuttama häiriö). Jos sähköinen häiriö on jatkuva, sähkömagneettiset aallot ovat olemassa jatkuvasti ja seuraavat niitä tiiviisti etenemisen aikana, kuten kuvassa 5 esitetyssä kaksoiskartioantennissa on esitetty. Kun sähkömagneettiset aallot ovat siirtolinjojen ja antennien sisällä, niiden olemassaolo liittyy johtimen sisällä olevaan sähkövaraukseen. Kuitenkin, kun aallot säteilevät, ne muodostavat suljetun silmukan, eikä niiden olemassaoloa ylläpitävä varaus ole olemassa. Tämä johtaa meidät seuraavaan johtopäätökseen:
Kentän viritys vaatii varauksen kiihdytystä ja hidastusta, mutta kentän ylläpito ei vaadi varauksen kiihdytystä ja hidastusta.
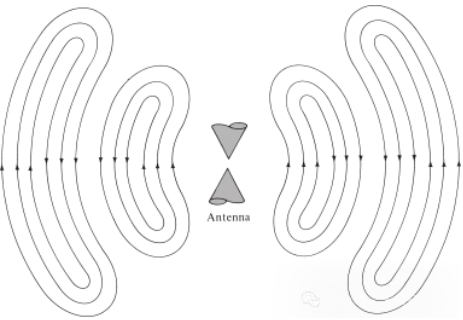
Kuva 5
3. Dipolisäteily
Yritämme selittää mekanismia, jolla sähkökentän viivat irtoavat antennista ja muodostavat vapaan tilan aaltoja, ja otamme esimerkkinä dipoliantennin. Vaikka se on yksinkertaistettu selitys, se antaa ihmisille myös mahdollisuuden nähdä intuitiivisesti vapaan tilan aaltojen syntyminen. Kuva 6(a) esittää dipolin kahden haaran väliin syntyvät sähkökentän viivat, kun sähkökentän viivat liikkuvat ulospäin λ∕4 syklin ensimmäisellä neljänneksellä. Oletetaan tässä esimerkissä, että muodostuneiden sähkökentän viivojen lukumäärä on 3. Syklin seuraavalla neljänneksellä alkuperäiset kolme sähkökentän viivaa liikkuvat vielä λ∕4 (yhteensä λ∕2 lähtöpisteestä), ja johtimen varaustiheys alkaa pienentyä. Sen voidaan katsoa muodostuvan vastakkaisten varausten myötä, jotka kumoavat johtimen varaukset syklin ensimmäisen puoliskon lopussa. Vastakkaisten varausten synnyttämät sähkökentän viivat ovat 3 ja liikkuvat matkan λ∕4, mitä katkoviivat kuvaavat kuvassa 6(b).
Lopputuloksena on, että ensimmäisellä λ∕4-etäisyydellä on kolme alaspäin suuntautuvaa sähkökenttäviivaa ja toisella λ∕4-etäisyydellä sama määrä ylöspäin suuntautuvia sähkökenttäviivoja. Koska antennissa ei ole nettovarausta, sähkökenttäviivat on pakotettava irtoamaan johtimesta ja yhdistymään muodostaen suljetun silmukan. Tämä on esitetty kuvassa 6(c). Toisella puoliskolla noudatetaan samaa fysikaalista prosessia, mutta on huomattava, että suunta on päinvastainen. Tämän jälkeen prosessi toistuu ja jatkuu loputtomiin, muodostaen kuvan 4 kaltaisen sähkökenttäjakauman.
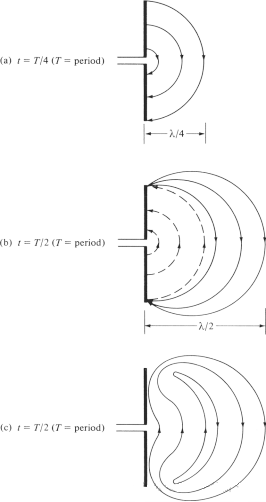
Kuva 6
Lisätietoja antenneista saat osoitteesta:
Julkaisun aika: 20. kesäkuuta 2024










